Fellow Reflections

Samuel Olivier’s father, uncles and grandparents were engineers and scientists, so he may have been fated to enter a similar field. But he also liked that engineering could improve people’s lives.

The first of three Lawrence Livermore National Laboratory internships as a Texas A&M University undergraduate, however, “really changed things for me,” says Olivier, now a Department of Energy Computational Science Graduate Fellowship (DOE CSGF) recipient. He worked on computer models of the Big Bang and supernovae reactions that produced the universe’s elements. “It was eye-opening to see the prevalence of computational science,” he says. Rather than work in a lab or the field, “I could use math and computers to do all the science I wanted.”

Olivier returned to Texas and did undergraduate research in a group devoted to computational science. That led to his third Livermore internship and the subject that still occupies him as a nuclear engineering doctoral candidate at the University of California, Berkeley.

Olivier focuses on the radiation transport equation, which calculates the release and absorption of heat as atoms split in nuclear reactors – or in processes designed to meld atomic nuclei, such as inertial confinement fusion (ICF). In ICF, as conducted at Livermore’s National Ignition Facility, powerful lasers enter a dime-sized tube, usually made of gold, and produce X-rays that bathe a BB-sized capsule filled with frozen hydrogen isotopes. The X-rays burn the capsule, compressing the hydrogen plasma enough to fuse nuclei and release tremendous energy. X-rays that emerge from this radiative heat transfer affect the momentum that squeezes the hydrogen, Olivier says.

The radiation transport equation, however, depends on seven variables arising from space, direction, energy and time. For ICF, it also must couple to the plasma’s movement and temperature, which behave in difficult-to-predict ways. This nonlinearity is the main hurdle to adapting techniques developed for fission reactor models – the focus of most radiation transport research – for ICF.

“Solving the transport equation is extremely taxing on even the biggest computers,” Olivier says. Most methods guess at answers, then iteratively refine them to an acceptable accuracy – a protracted process. Techniques to accelerate it demand precise discretization, which casts a mesh of points through the modeled region – an ICF capsule’s interior, for example – and calculates physics at each. Radiation transport calculations can consume 90 percent of the runtime and memory use for ICF models, Olivier says.

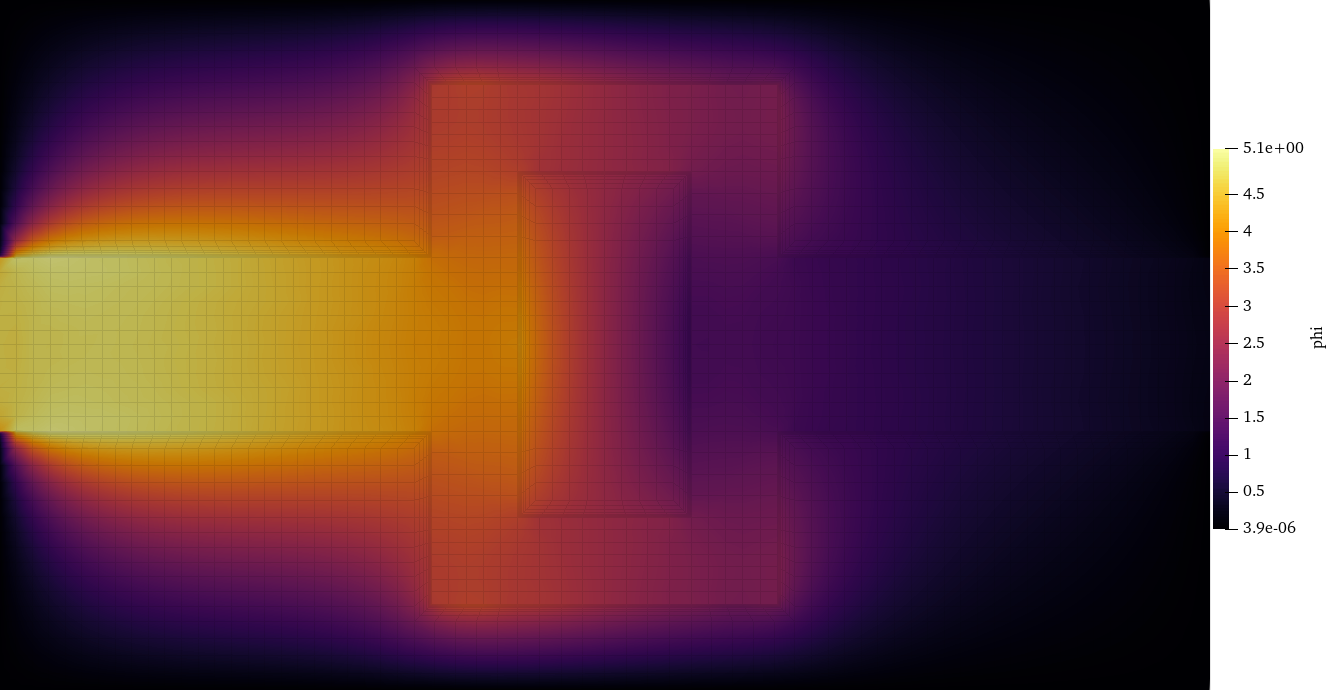
For solutions, Olivier worked with his advisor, Rachel Slaybaugh, and Livermore scientists Terry Haut and Ben Yee to resurrect the Variable Eddington Factor (VEF) method, a 1960s-vintage algorithm the nuclear energy community considered too unusual to use.

To sidestep the discretization issue, VEF separates meshes for radiation transport and for equations that accelerate the calculations. The technique works with faster and more precise high-order discretizations that will underlie a next-generation ICF model. It also addresses nonlinearity, coupling those equations to the less-demanding VEF method, and makes curved, rather than straight-edged, meshes feasible.

“A big impact of my work is that I convinced people at the labs to consider this and now we’re actively trying to put it into the next-generation code,” Olivier says. With Haut and Yee, he’s implemented VEF in a research program. Now, with Olivier’s input, the Livermore team is bringing it into a usable ICF model.

Olivier also is addressing VEF method flaws and devoted a 2020 practicum to one: high-order discretization results in equations that are computationally expensive to solve. He tested many techniques without finding one that would work when the code is extended to real-world problems.

“I was banging my head against the wall,” Olivier says, so he set the problem aside. He returned to it in January with an idea Haut had suggested. “I finally got around to thinking about it,” Olivier says, and found two methods that efficiently solve the equations. He’s writing papers and doing a third Livermore practicum to combine these techniques with a VEF-based algorithm Yee has devised and implemented in a research code.

Olivier also did a 2019 practicum at Los Alamos National Laboratory, where he tested an idea from James Warsa: use VEF in Capsaicin, a lab-produced radiation transport code, to solve equations at individual mesh elements rather than globally to run faster on supercomputers. Olivier found the technique offered few advantages but gained new relationships and lessons in working with a major code.

Olivier expects to graduate in 2022. Given his national laboratory work, it’s no surprise that he’ll next seek a postdoctoral fellowship with one of them.

Image caption: A transport solution for the energy density in the crooked-pipe problem, a challenging proxy problem from inertial confinement fusion that models radiation flowing through an optically thin pipe. Brighter colors represent greater energy density. Radiation enters the pipe at the left, encountering a barrier that scatters it, keeping most of it in the pipe. The dark-colored, low energy-density region at right is a barrier-induced “shadow.” A method to accelerate calculations, such as the Variable Eddington Factor, is necessary to converge on a high-resolution solution to the problem in a practical amount of time. Credit: Samuel Olivier.